La projection conique conforme de Lambert : mathématicien, astronome touche à tout du XVIII siècle.

    Petit rappel une projection conforme est une projection qui conserve les angles.

   Un peu d'histoire : Initialement les cartes militaires n'étaient pas conformes. C'est à dire que la valeur des angles n'était pas fidèle (voir sur le site la différence entre une carte conforme et une carte équivalente).

Quoi de pire pour un artificier que de viser un objectif non visible à l’œil nu sans connaitre avec précision son azimut ?

     Le problème s'est posé durant la première guerre mondiale pour l'armée française qui ne pouvait pas orienter ses canons avec précision sur des cibles invisibles depuis le canon. L'adoption des projections Lambert c'est alors vite généralisées !

     L’axe du cône est sur l’axe des pôles, et l’ellipsoïde retenu sera soit le Clarke 1880-IGN pour les Lambert 1,2,3,4 et Carto (ou étendu), WGS84 pour le Lambert 93 et les petits nouveaux CC42 à CC50.

     Dans le cas des projections Lambert utilisées en France, il s'agit d'une projection sécante : le cône coupe 2 fois le globe terrestre au niveau de 2 parallèles Φ1 et Φ2 . Le parallèle de référence à la projection est le parallèle médian Φ0 = (Φ1+ Φ2) /2 ou Φ1 est la latitude basse et Φ2 la latitude haute.

     Les parallèles Φ1 et Φ2 sont dit automécoïques car ils sont à la fois sur le globe et sur le plan de projection. C'est à dire que les points qui les constituent ne seront pas modifiés par la projection. En clair les longueurs mesurées dessus seront justes.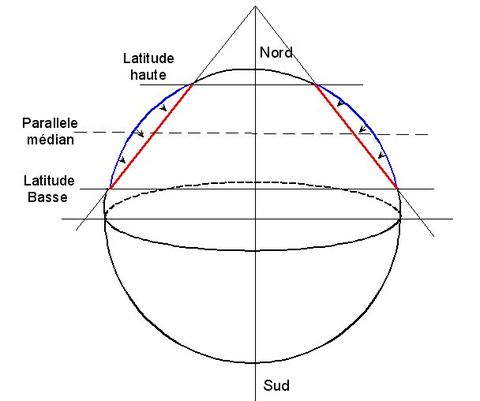

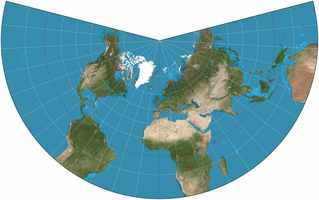
La surface déroulée après projection sera plane et se présentera ainsi:

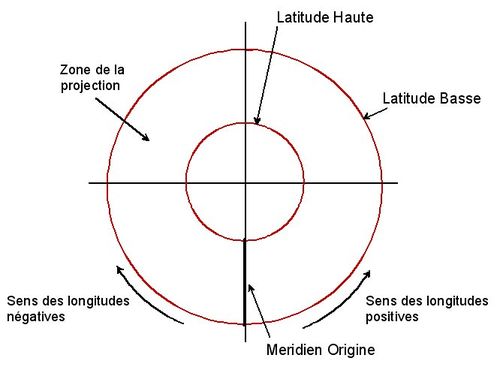
     Les longitudes comme sur toutes les projections seront comptées positives à l'Est à partir d'un méridien d'origine.

    Dans le cas plus particulier du Lambert on va recréer un repère orthonormé gradué en m ou km dont les 2 axes X et Y seront respectivement perpendiculaires et parallèles au méridien d'origine et à une distance X0 et Y0 du méridien de Paris et du parallèle médian.

    L'intérêt de positionner ces 2 axes plus au Sud que la limite de la carte et plus à l'ouest que la pointe de Bretagne, garanti d'avoir toujours des coordonnées cartographiques en m ou km positives.

     Les coordonnées Lambert sont 2 distances: X qui est la distance "horizontale" de l'axe X0 et Y la distance "verticale" de l'axe Y0

    Il est donc très facile de calculer grâce à Pythagore des distances entre 2 points ou des angles de direction (azimut). Les erreurs liées au mode de projection sont minimes.

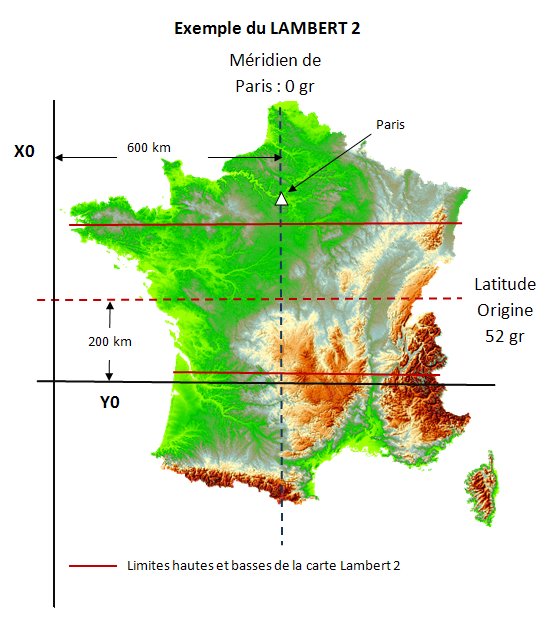
     Moins la distance entre les 2 parallèles automécoïques est grande, moins la projection génèrera des distorsions, et le calcul des distances sera aisé. Cette constations est à l'origine des différentes projection Lambert.

     Voici les caractéristiques des projections Lambert I, II, III, IV et II étendue qui s'appuie sur l'ellipsoïde de Clarke 1880 IGN, et qui ont pour origine le méridien de Paris.

 

Depuis le 26 décembre 2000 le Lambert 93 est la projection officielle en France métropolitaine. Dans les faits le Lambert 2 étendu est toujours très utilisé 10 ans après dans les travaux publics ou chez les opérateurs de téléphonie par exemple. Elle a l’avantage de couvrir l’étendue entière du territoire en une seule projection. La majeure partie des outils de SIG sont basés sur le Lambert 2 étendu bien que l’évolution vers le Lambert 93 soit en route.

 

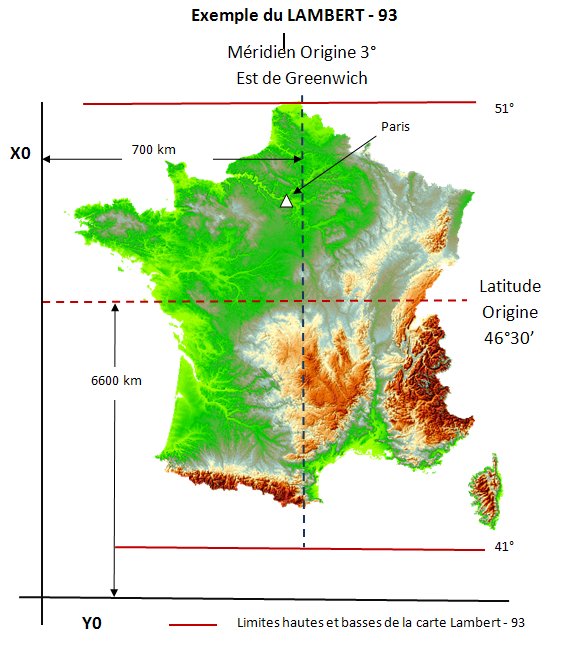
Exemples : coordonnées Lambert 2 étendue du centre de Pau (dép. 64) X=379 464m  Y= 1 814 349m. En Lambert 93 le même point est coté : X= 425882m et Y= 6 250 091m

Dans le système WGS84 et l'ellipsoïde WGS84 les coordonnées seraient : 43° 17' 50,01" Nord et 0° 22' 37,43" Ouest.

Dans le système ED50 Européen et l'ellipsoïde Hayford 1909 les coordonnées seraient : 43° 17' 53,87" Nord et 0° 22' 33,10" Ouest

En fait les plus précises sont les Lambert 93 et WGS84 qui utilisent des ellipsoïdes déterminées par imagerie satellite.

Les ellipsoïdes de Clarke et d'Hayford ont été déterminés par triangulation depuis le Panthéon de Paris pour Clarke et Posdam pour Hayford.

 

Il existe d'autres projections Lambert pour la France:

   Les Carto :

    Les Lambert 1-2-3-4 Carto sont les mêmes que les Lambert 1-2-3-4 mais sur la valeur de Y on rajoute un chiffre à gauche qui correspond au numéro du type de projection soit 1-2-3-4

         Exemple : les coordonnées du centre de Pau en Lambert 3 sont : X=379841 et Y=114445 en Lambert 3 Carto les coordonnées deviennent X=379841 et Y=3114445. L'intérêt est qu’en voyant uniquement les coordonnées on sait identifier quelle zone Lambert a servie à la projection.

   Les projections CCxx :  

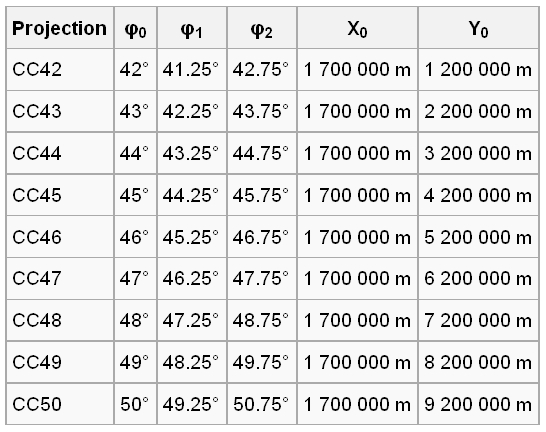
     Les 9 projections CC42 à CC50 Sont des projections Lambert s'appuyant sur le Lambert 93 mais couvrant une surface plus petite. Il y a uniquement entre les 2 parallèles automécoïques que 1°30'. La précision de ces cartes est donc accrue avec quasiment pas de distorsion.

     Voici une méthode pour retrouver les paramètres en fonction de numéro de la projection. Le numéro de projection NP correspond à 42 dans la projection CC42 par exemple.

       Latitude origine (ou médiane) = NP

       Zone d'application = 111 km au-dessus ou au-dessous du parallèle d'origine

       Parallèles automécoïques = + ou - 0,75° par rapport à la parallèle origine

       Méridien origine = 3° Est de Greenwich

       Axe origine des X à 1 700 000 m du méridien d'origine

       Axe origine des Y = ((NP-41) x 1 000 000) +200 000 en mètres

     Voici ci-dessous le tableau complet de leurs caractéristiques.

     En voyant tous ces types de coordonnées la crainte va être de savoir s'il est possible de procéder à des conversions d'un système à un autre. Oui c'est possible. Avec le logiciel Circé téléchargeable sur le site de l'IGN on peut passer sans problème d'un système à un autre, changer de géoïde, d'unité de mesure et cela très facilement. En voici le lien