Ellipsoïdes et Géoïde. Avant de commencer à projeter sur papier notre monde 3D,  il nous faut bien connaître la forme de notre globe.

Au cours de sa création la terre à subit un aplatissement de 21 km sur les rayons Nord Sud. Cette déformation est suffisamment importante pour générer des erreurs importantes sur la transformation de coordonnées géographiques en coordonnées planes sur une carte.

    Ellipsoïde :

    Des mathématiciens ont travaillés sur la modélisation du globe et l’ont rapproché à un ellipsoïde, c'est-à-dire au volume qu’aurait créé une ellipse tournant sur elle-même. La chose ne devait pas être si simple que cela car en France il est commun d’utiliser 4 modélisations qui correspondent en fait à 4 systèmes géodésiques qui regroupent un ellipsoïde propre, un méridien origine (Paris, Posdam, Greenwich), et une unité d'angle (degré ou grade )

    Clarke 1880 associé au système NTF (Nouvelle Triangulation Française)

    Hayford 1909 associé au système ED50 (système Européen mis en place après la seconde guerre mondiale)

    IAG GRS80 associé au système RGF93 (en France en remplacement du NTF)

    WGS84 associé au système du même nom WGS84 très semblable au précèdent, mis en place par le département de la défense américain.( Différence de 0,1mm sur l’axe b du globe avec le système IAG GR80)

    Ces deux derniers ont bénéficiés  des observations par satellites et sont les  plus précis. Ils sont utilisés notamment par les systèmes GPS.

Ci-dessous un petit tableau récapitulatif :

Relations importantes pour un ellipsoïde donné :  1 / f = a  / ( a - b )        e = racine carrée de ( ( a² - b² ) / a² )

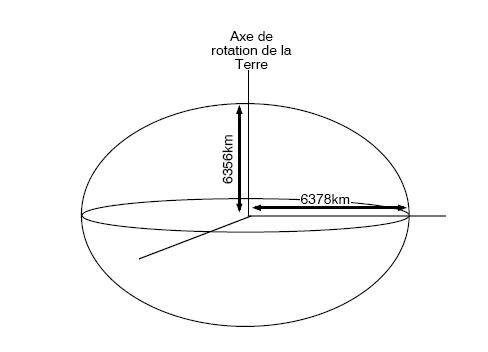
Rayon équatorial 6378 km = a  et rayon polaire 6356 km = b     a - b = 22 km

L’ellipsoïde étant choisie il « suffit » de tracer la perpendiculaire du point que l’on veut représenter du globe sur l’ellipsoïde pour avoir les coordonnées sur l'ellipsoïde. Exemple la Suisse utilise le Bessel 1841. Des grands pays pourront par aussi en utiliser plusieurs pour augmenter la précision de leur cartographie.

Il existe une grande quantité ellipsoïde car pour augmenter la précision, à l'échelle d'un pays, on peut fort bien déterminer un ellipsoïde spécifique qui sera par la suite au moment d'effectuer des projections dessus plus précis.

Géoïde :

    Le Géoïde quant à lui est une représentation du globe terrestre qui est une surface sur laquelle tous les points sont soumis à la même force de gravitation. En clair sur cette surface l’eau ne coule pas. Il s’agit d’une surface équipotentielle de la pesanteur. Cette surface est très irrégulière car elle déformée par une répartition inégale des masses dans et sur le globe terrestre.

    La surface des océans et des mers donnant sur ces océans font partie de la surface du géoïde (Attention : une mer fermée n'est pas sur le geoïde. La mer morte est 420 m en dessous du géoïde).  A proximité d’une chaine de montagne ou d’une chaine volcanique le géoïde sera déformé.

    Par simplification un point du globe terrestre est considéré fixe bien qu'il soit soumis aux marées terrestres qui provoquent des mouvements d'aller et retour d'une amplitude inférieure à 30 cm et à la tectonique des plaques qui génère des déplacements de 10 cm par an en fonction de la région du globe.

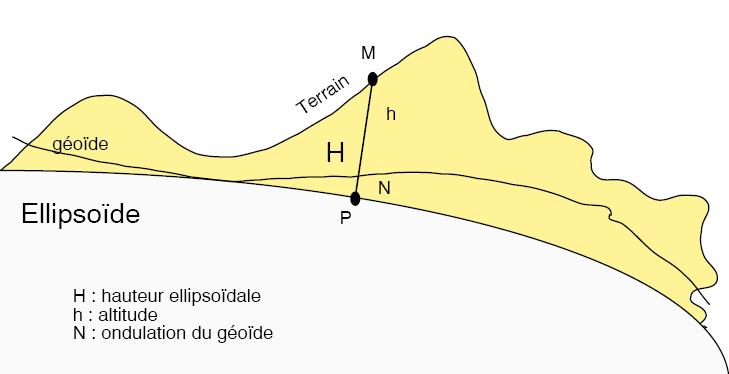
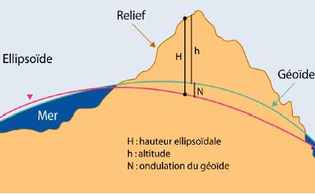
    On perçoit très bien sur ce schéma la différence entre h qui est l'altitude et H la distance à ellipsoïde. N s'appelle ondulation du géoïde. Elle est inférieure à 100m pour tout le globe.

    C’est à partir du géoïde que l’on mesure les altitudes :

    Le Mt Blanc est 4807m du géoïde terrestre. Cela fait quand même plus classe que de dire 4807m au-dessus du niveau de la mer !

    Il peut y avoir entre l’ellipsoïde et le géoïde des différences de formes allant jusqu’à 100metres.

    L'ellipsoïde est la figure géométrique qui se rapproche le plus du géoïde. Les méridiens seront donc tous des ellipses de même périmètre et les parallèles seront tous des cercles.

    On comprend donc mieux que pour dessiner notre carte il sera plus facile de projeter les points que l’on souhaite représenter à partir d'une ellipsoïde bien maitrisée et ensuite effectuer notre projection vers notre système 2D qui est la carte papier ou l’image sur un écran de PC.

    Il est à remarquer que chaque pays aura ses systèmes géodésiques propres et utilisera des ellipsoïdes locaux qui seront les plus proches du géoïde local.

    Un système d'équations permettra alors la transformation d'un environnement 3D vers un environnement 2D. Il est facile de les retrouver sur Internet, plus difficile de les utiliser, mais là n'est pas le propos ici.

Pour résumer: l'ellipsoïde modélise la forme de notre globe. Elle ne modélise pas notre relief. Le géoïde lui modélise une surface où tous les points subissent le même effet de la gravitation. C'est une surface équipotentielle.

     Le modèle gravitationnel officiel de la Terre EGM2008 a été rendu public par l'équipe de développement EGM de la National Geospatial-Intelligence Agency (NGA) des États-Unis.

    La France a lancé en 1975 le satellite Starlette et en 93 le satellite Stella. Ce sont 2 boules passives de 47 kg équipées de 60 rétroréflecteurs (qui renvoie sur la source un rayon lumineux ou laser reçu). Ils sont sur des orbites à 800km. Ils permettent de mesurer par les variations de leurs orbites les variations de la gravitation à la verticale de leurs lieux de passage.