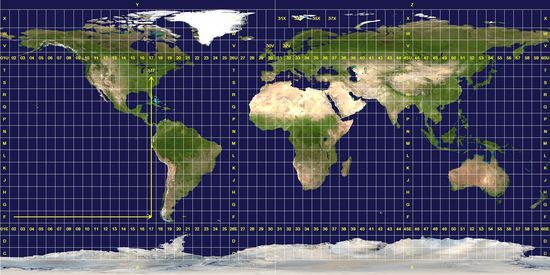
Les Projections Conformes de Mercator. Coordonnées UTM (Universal Transverse Mercator). La projection de Mercator est une projection cylindrique, sur un cylindre horizontal dont l’axe est perpendiculaire à l’axe des pôles. La projection Mercator est conforme et tous les méridiens sont parallèles.
Cela bien sûr interdit la représentation des zones polaires (où par définition les méridiens se croisent) et génère des distorsions importantes de surface. L’Amérique du Sud plus petite que le Groenland par exemple.
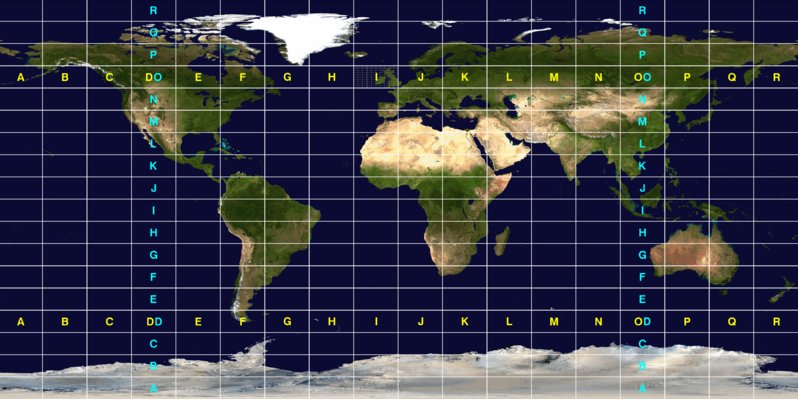
Le globe est alors divisé en 60 fuseaux verticaux de 6° (tranche de méridiens espacés de 6°) et en 20 bandes parallèles de 8° sauf la plus au Nord qui fait 12° de large. Elles sont désignées du Nord au Sud par une lettre de l'alphabet de C à X en utilisant pas les lettres I et O
Pour une carte de grande résolution cliquez sur la carte
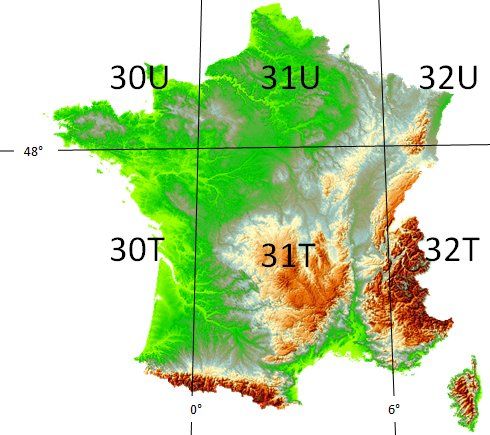
La France est partagée par 3 fuseaux et 6 bandes UTM : zone 30 de -6° à 0° T et U ; zone 31 de 0° à 6° T et U ; zone 32 de 6° à 12° T et U.
Etant conforme cette projection est très utile pour les marins qui peuvent facilement définir leur cap par une route toute droite qui coupe tous les méridiens avec le même angle (loxodromie), qui ne sera pas cependant la route la plus courte qui est en fait un arc de cercle ayant pour centre le centre du globe et pour extrémité les points de départ et d’arrivée du trajet (orthodromie).
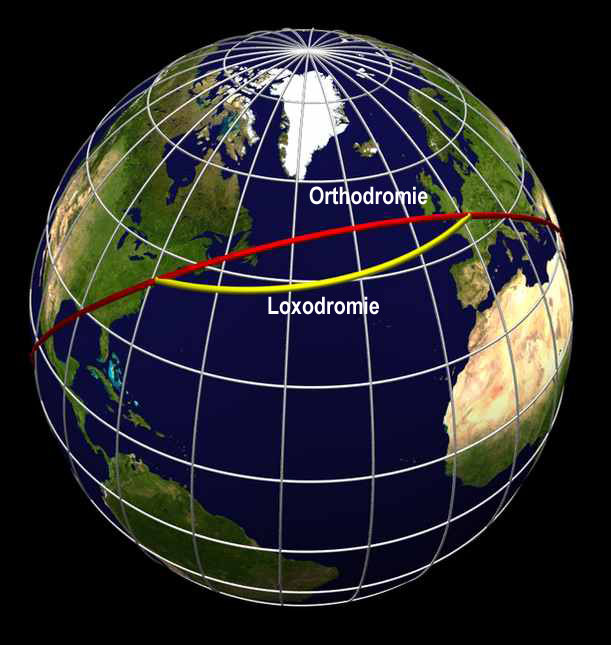
Dans le cas de loxodromie, la trajectoire coupe les méridiens toujours avec le même angle. Un navire qui suit une loxodromie ne change pas de cap de tout son trajet. Pour orthodromie ce n'est plus le cas comme on le voit sur le schéma. C'est le chemin le plus court entre 2 points du globe. C'est le bout de ficelle que l'on temps sur un globe entre 2 points. C'est la trajectoire que suivront les avions par économie de carburant et de temps.
Les coordonnées cartographiques sont données de la manière suivante :
Les abscisses sur l’axe horizontal sont mesurés d’Ouest en Est en mètre de telle manière que le méridien central du fuseau, c'est-à-dire celui qui est à 3° du bord Ouest ou Est (le fuseau faisant 6°) soit sur l’abscisse 500 000m. Les valeurs des abscisses seront entre 167 000m et 833 000m.
Les ordonnées de l'hémisphère Nord sont mesurées en mètre depuis l’équateur.
Sur l'hémisphère Sud il faut faire 10 000 000 moins la distance en mètre depuis l'équateur. Elles sont donc toujours positives.
Il faut toujours préciser le nom de l'hémisphère Sud ou Nord ou la bande horizontale en même temps que ses coordonnées pour bien situer un point car il pourrait facilement y avoir confusion.
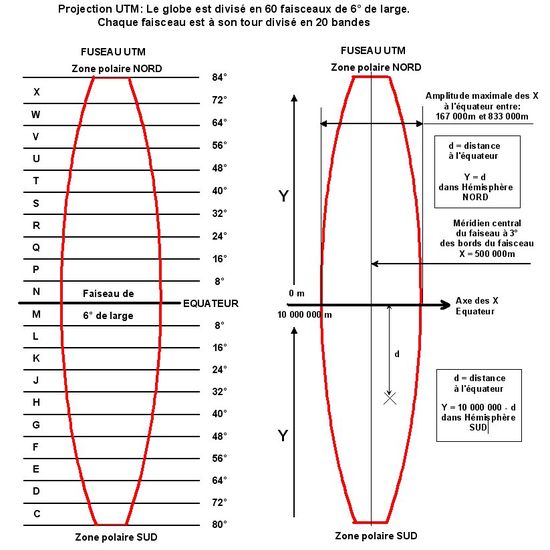
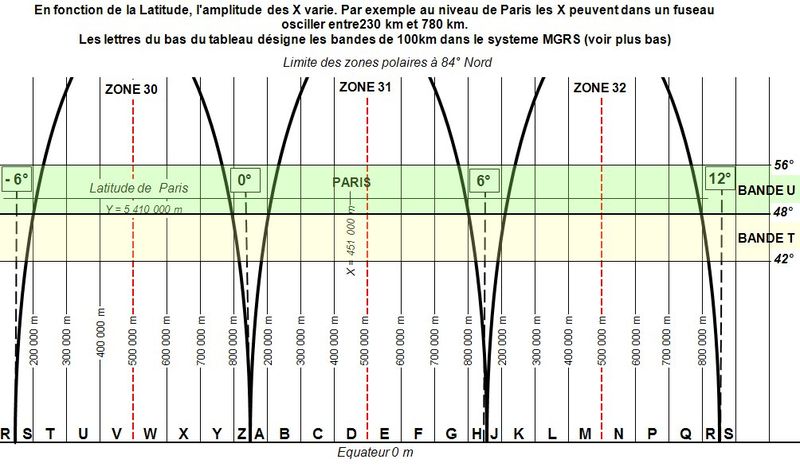
On retrouve donc comme dans la projection Lambert précédente un repère orthonormé ou il est facile de se repérer et de faire des calculs, à la différence que la France est partagée en 3 faisceaux et qu’il est beaucoup plus difficile de faire ces calculs lorsque l’on est à cheval sur 2 faisceaux. En Lambert 2 étendu ou RGF93 la zone couvre largement tout le pays.
Une remarque importante : La projection de Mercator et la projection conique Lambert étant toutes les deux conformes (conservation des angles), il est possible sur une carte en projection Lambert de tracer les zones Mercator sur le même support sans surcharger la carte. C’est ce que fait l’IGN avec les cartes au 1/25000.
Une variante de l’UTM : le système MGRS
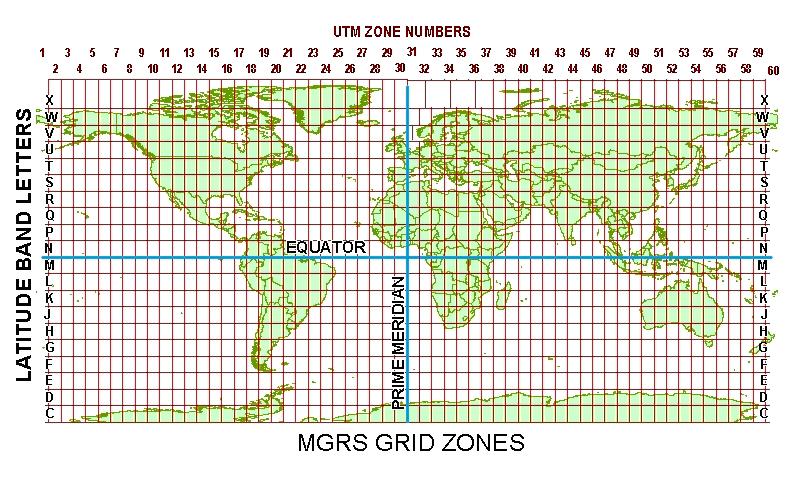
Il s'appuie sur le système UTM vu précédemment, avec les fuseaux de 6° et les bandes de 8° de haut. Il est utilisé par les militaires de l'OTAN, les radioamateurs et les randonneurs. En effet certaines cartes portent des informations MGRS et dans certains pays, les cartes papiers pour randonneurs correspondent au zonage MGRS
.
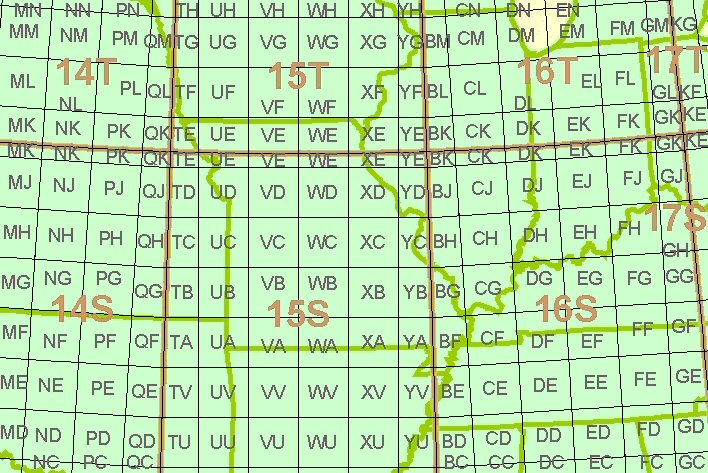Dans les fuseaux, on va faire des carrés de 100 km de coté qui seront par une codification un peu compliquée référencés par 2 lettres. Ensuite on positionne les coordonnées X et Y du point dans ce carré. Pour les zones polaires au-delà de 84° Nord et 80° Sud on abandonne les projections cylindriques pour une projection azimutale. Nous avons fait un tutoriel avec un exemple pour tout savoir sur les coordonnées MGRS.
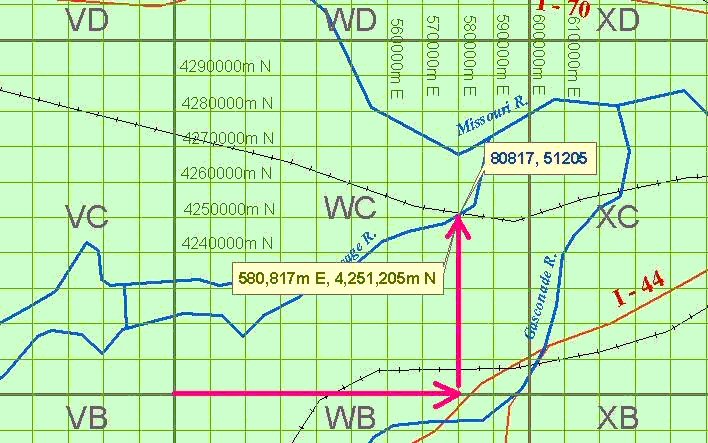
Ce type de coordonnées défini un point par une seule expression, mais peut définir des zones carrées de 10m, 100m, 1km, 10km ou 100km de coté en fonction de la précision souhaitée.
Voici pour le centre-ville de Pau les coordonnées WGS84: 43° 17' 50,01" Nord et -0° 22' 37,43" Ouest en UTM on a: 30T X = 712762 Y = 4797163 Nord
En MGRS cela donne: 30T YN 12762 97163 (ou en collé 30TYN1276297163) on retrouve dans ces coordonnées: 30T qui est la zone de 6° x 12°; YN est le carré de 100 km de coté ( voir tutoriel), 12762 le X à l'intérieur du carré de 100km et 97163 le Y . On peut constater que cela correspond au 5 derniers chiffres des X et Y UTM en mètres.
Si nous voulons avoir uniquement une précision à 100 m prés, il suffit d'enlever les chiffres des mètres et des décimètres à la coordonnée précédente, et nous avons alors 30TYN127971
Voici ici un lien pour atteindre un convertisseur en ligne pour ce type de coordonnées.
Un système intéressant les radioamateurs : le système Locator.
Le système est représenté souvent avec une projection UTM. En réalité il s'agit d'un système permettant de convertir les coordonnées géographiques en une seule expression contenant la Longitude et la Latitude. Le globe est alors divisé avec des fuseaux de 20° en longitude et des bandes horizontales de 10° de latitude.
Chaque zone est nommée par 2 lettres. Selon l'horizontale de A à R dans le sens Ouest Est et en partant de 180° Greenwich, et dans le sens vertical de A à R dans le sens Sud Nord.
En latitude on démarre du pôle Sud pour aller au pôle Nord, c'est à dire que les zones polaires sont couvertes par ce type de conversion de coordonnée qui est indépendant d'une méthode de projection, contrairement au MGRS tributaire de la projection UTM.
Chaque carré de 20° x 10° de côté est divisé en 100 petit carrés de 2° x 1° numérotés de 00 à 99. La numérotation se fait toujours de bas en haut et de gauche à droite en mettant le chiffre des colonnes en premier.
Chaque carré de 2° x 1° est divisé en 24 colonnes et 24 lignes faisant des carrés de 0° 5' x 0° 2,5' nommés de AA à XX. La numérotation se fait toujours de bas en haut et de gauche à droite en mettant la lettre des colonnes en premier.
Je ne peux que conseiller le site de F6GCI qui apportera des schémas de grilles et un exemple avec en plus un convertisseur de coordonnées en ligne pour trouver les coordonnées Locator. Une précision : avoir les coordonnées de départ en degrés décimaux et mettre un point comme séparateur après les degrés. Pour les curieux visitez son site il y a plein de choses intéressantes !
Reprenant en exemple les coordonnées du centre de PAU. Nous avons: Long = -0.37586 et Lat = 43.29830 le positionnement Locator serait IN93TH
Le système GEOREF
Comme le système Locator, le système GEOREF est un moyen de convertir les coordonnées géographiques en une seule expression. Peu utilisé aujourd’hui, il servait initialement à la navigation aérienne. Très simple d'utilisation car on va passer par une étape d'un carré de 1° de côté, il est basé sur les mêmes principes que le système précédent avec un découpage du globe en 24 fuseaux de 15° et un découpage en 12 bandes de 15°
Les fuseaux sont nommés par les lettres de l'alphabet sans le I ni le O, les bandes sont nommées par les lettres de A à M sans le I. Le couple de lettre est constitué en premier de la lettre désignant les colonnes et ensuite celle de la bande.
Chaque carré de 15° de côté est subdivisé en petits carrés de 1 degré en utilisant 15 lettres dans les 2 directions de A à Q en ôtant le I. A à Q horizontalement et A à Q verticalement. La lettre des colonnes en premier dans le couple de lettre.
Dans chaque petit carré de 1 degré on ajoute alors les 2chiffres en minutes en horizontal et les 2 chiffres en minutes verticalement. Nous avons alors une précision à la minute prés. Les coordonnées se présentent alors de la manière suivante :
NKGB2515 ou NK est le carré de 15° de côté, GB le carré de 1° de côté et 25 et 15 respectivement la longitude et latitude en minute dans le carré d'un 1° de côté.
Il est bien sur possible d'augmenter la précision en rajoutant des fractions décimales de minutes sur les 2 axes. Par exemple pour une précision de 0,01 minutes on rajoutera 2 chiffres à la longitude et à la latitude. Nous aurions alors une coordonnée de la forme suivante : NKGB25861524 ou 2586 veut dire 25,86' et 1524 correspondrait à 15,24'
Le lien suivant permet de convertir aussi en coordonnées GEOREF
Ainsi Pau qui n'a toujours pas bougé et qui se trouve en Lat 43,29830° et Lon -0,37586° est en GEOREF avec une précision de 0,01' en MJQP37441789
La projection des serveurs de cartographie sur internet:
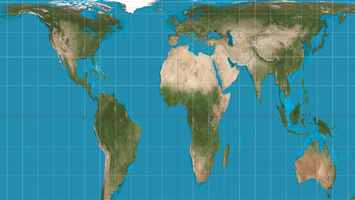
Une autre variante de la projection de Mercator est la projection cylindrique équidistante. Sur cette carte les parallèles sont équidistantes ainsi que les méridiens. C’est une projection cylindrique sur un cylindre dont l’axe est parallèle à l’axe terrestre. C’est la projection utilisée sur les serveurs de cartographie comme Google-Earth ou Geoportail. Contrairement à l’UTM ce n’est pas une projection conforme. Elle dilate horizontalement les fortes latitudes.
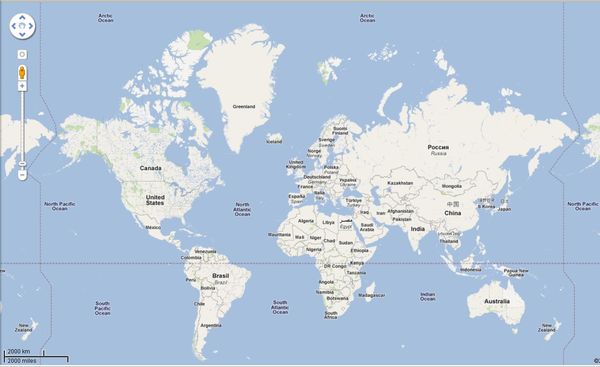
Ici une copie d'écran du site Google Maps. On pourra comparer avec la carte qui se trouve au haut de cette page les déformations importantes des zones polaires. Les sites de Mapometer et Openstreetmap fonctionnent sur ce principe. L'Argentine 2 780 000 km² est ici moins de 3 fois plus petite que le Groenland 2 166 000 km². La Russie représentent en réalité un peu moins du double que les USA et un peu moins du double que la Chine.
